I’m always on the lookout for ways to speed up our project work and also some of the inner workings of Papervision3D, and I must admit, sometimes it reaches fairly obsessive levels, bordering on unhealthy. In fact sometimes the minor optimisations are so insignificant, it can just be an exercise in problem solving. Which let’s face it, we all do from time to time just for fun, right? 😉
The latest target for my attention is the triangle / rectangle intersection check that happens just before rendering. It’s way after any of the clever 3D stuff, we’re just literally looking at whether the 2D triangle we’re about to draw is within the rectangle that represents our screen.
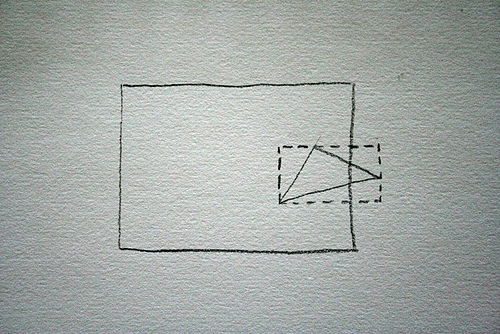
The current check is a simple bounding rectangle check. The bounding rectangle for the triangle is calculated and we use a simple intersect check for the two rectangles. Which is simple and fast. But it was bothering me that huge offscreen triangles were not getting culled because their bounding rectangle overlapped with the viewport rectangle.
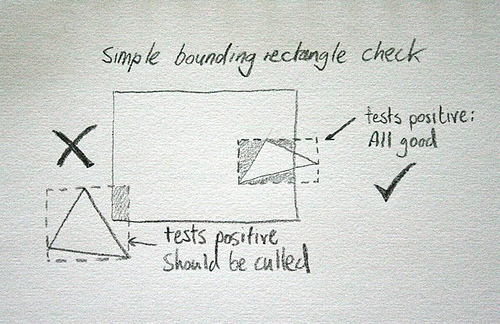
So how do you accurately check that a triangle is intersecting a rectangle? Here’s one way :
1) Check if any of the triangle’s points are within the rectangle, if yes then intersection is true.
2) Check if any of the triangle’s lines intersect any of the rectangle’s lines, if yes then intersection is true.
Check 1 is relatively simple, but if no points are within the rectangle, we have to move to check 2, and that means we have to check each of the 3 lines in the triangle with each of the 4 lines of the rectangle, 12 line intersection checks altogether. Which just felt a bit dirty to me.
But then I got to thinking, this rectangle is an AABB (or axis-aligned bounding box, which basically means that it’s not rotated), so that should make things a little easier. And I developed this little technique loosely based on existing systems but I haven’t seen anything exactly like this before. I’m not sure if it’s the best way but it seems fast and accurate to me! Here’s how it works :
1) take the first line of the triangle
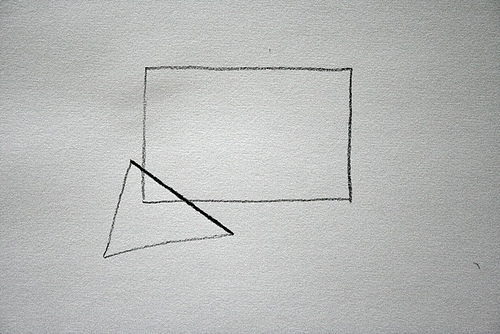
2) calculate its equation and then work out the y position that it intersects the left and right edges of the rectangle
3) take the maximum and minimum y bounds of those two intersection points and calculate the overlap between those and the max and min y values of the line.
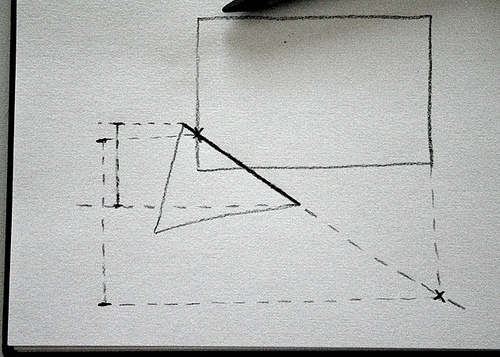
4) if these new overlapping min and max y values overlap the top and bottom of the rectangle then the line (and therefore the triangle) must intersect the rectangle, so return true.
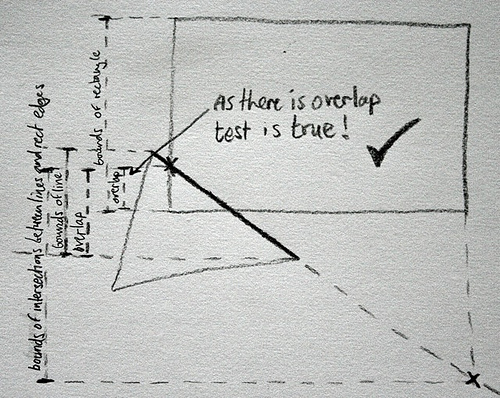
5) Otherwise move on to the next line of the triangle and try again.
It seems to be much more accurate than the existing bounding rectangle check and for positives is 30% faster. For negatives it’s about the same or a tiny bit slower. The only innaccuracy I’ve found is if the triangle is entirely containing the rectangle it returns negative. And also I should put in a check for vertical lines and do a simpler check on those.
But my challenge to you! Can you get this to be slicker / faster? I’m sure there are some maths wizards out there. Full code below and you can even fork it and have a play at the rather awesome Wonderfl
I realise that you could unroll the method call to triangleAABBIntersectionTest but I’m more interested in improvements to the maths/logic.
Good luck!
package
{
import flash.display.Graphics;
import flash.display.Sprite;
import flash.events.MouseEvent;
import flash.geom.Point;
import flash.geom.Rectangle;
import flash.text.TextField;
import flash.text.TextFormat;
import flash.utils.getTimer;
[SWF(frameRate="100", backgroundColor="0x000000", width="500", height="500")]
public class TriangleAABBSpeedTest extends Sprite
{
public var outputText : TextField;
public function TriangleAABBSpeedTest()
{
super();
outputText = new TextField();
x = y = 250;
outputText.defaultTextFormat = new TextFormat("Arial");
outputText.textColor = 0xffffff;
outputText.text = "Click to start test";
outputText.x = outputText.y = -250;
outputText.width = 500;
addChild(outputText);
stage.addEventListener(MouseEvent.MOUSE_DOWN, startTest);
}
// I'm thinking that storing these values as properties rather than declaring them as local vars
// should be faster...
private var x0 : Number;
private var y0 : Number;
private var x1 : Number;
private var y1 : Number;
private var x2 : Number;
private var y2 : Number;
private var l : Number;
private var r : Number;
private var t : Number;
private var b : Number;
private var top_intersection:Number ;
private var bottom_intersection : Number;
private var toptrianglepoint : Number;
private var bottomtrianglepoint : Number;
private var m: Number;
private var c : Number
// THESE ARE THE TWO FUNCTIONS YOU CAN OPTIMISE.
// I realise that you could inline the lineRectangleIntersect method, but I'd rather not do that just yet...
// I'm looking for maths/logic improvements.
public function triangleAABBIntersectionTest(rect:Rectangle, vertex0:Point, vertex1:Point, vertex2:Point ) : Boolean
{
// YOU MUST LEAVE THESE DECLARATIONS; they simulate necessary data exchange within PV3D
l = rect.left;
r = rect.right;
t = rect.top;
b = rect.bottom;
x0 = vertex0.x;
y0 = vertex0.y;
x1 = vertex1.x;
y1 = vertex1.y;
x2 = vertex2.x;
y2 = vertex2.y;
return lineRectangleIntersect(x0,y0,x1,y1)
|| lineRectangleIntersect(x1,y1,x2,y2)
|| lineRectangleIntersect(x2,y2,x0,y0);
}
public function lineRectangleIntersect(x0: Number,y0: Number,x1: Number,y1: Number):Boolean //, left:Number, right:Number, top:Number, bottom:Number) : Boolean
{
// Calculate m and c for the equation for the line (y = mx+c)
m = (y1-y0) / (x1-x0);
c = y0 -(m*x0);
// if the line is going up from right to left then the top intersect point is on the left
if(m>0)
{
top_intersection = (m*l + c);
bottom_intersection = (m*r + c);
}
// otherwise it's on the right
else
{
top_intersection = (m*r + c);
bottom_intersection = (m*l + c);
}
// work out the top and bottom extents for the triangle
if(y0toptrianglepoint ? top_intersection : toptrianglepoint;
botoverlap = bottom_intersection<bottomtrianglepoint ? bottom_intersection : bottomtrianglepoint;
// (topoverlap<botoverlap) :
// if the intersection isn't the right way up then we have no overlap
// (!((botoverlapb)) :
// If the bottom overlap is higher than the top of the rectangle or the top overlap is
// lower than the bottom of the rectangle we don't have intersection. So return the negative
// of that. Much faster than checking each of the points is within the bounds of the rectangle.
return (topoverlap<botoverlap) && (!((botoverlapb)));
}
public function startTest(e:MouseEvent = null) : void
{
var g : Graphics = graphics;
g.clear();
var cullingRect : Rectangle = new Rectangle(-100,-75,200,150);
var iterations : int = 100000;
var timerIntersecting : int = 0 ;
var timerNotIntersecting : int = 0 ;
var intersectCount : int = 0;
var v0 : Point = new Point();
var v1 : Point = new Point();
var v2 : Point = new Point();
var i : int = iterations;
while(--i>-1)
{
v0.x = Math.random()*400 - 200;
v0.y = Math.random()*400 - 200;
v1.x = v0.x+ (Math.random()*300 -150);
v1.y = v0.y+ (Math.random()*300 -150);
v2.x = v0.x+ (Math.random()*300 -150);
v2.y = v0.y+ (Math.random()*300 -150);
var startTimer : int = getTimer();
var intersecting : Boolean = triangleAABBIntersectionTest(cullingRect, v0, v1, v2);
if(intersecting)
{
timerIntersecting += (getTimer() - startTimer);
intersectCount++;
}
else
{
timerNotIntersecting += (getTimer() - startTimer);
}
if(i<300)
{
g.lineStyle(0,0x000000);
g.beginFill(intersecting ? 0x006600 : 0x660000,0.5);
g.moveTo(x0,y0);
g.lineTo(x1,y1);
g.lineTo(x2,y2);
g.lineTo(x0,y0);
g.endFill();
}
}
g.lineStyle(0,0xffffff,0.5);
g.drawRect(cullingRect.x, cullingRect.y, cullingRect.width, cullingRect.height);
outputText.text = "Average time per triangle : "+(timerIntersecting+timerNotIntersecting)/iterations;
outputText.appendText("nAverage time per intersecting triangle : "+(timerIntersecting)/intersectCount);
outputText.appendText("nAverage time per non-intersecting triangle : "+(timerNotIntersecting)/(iterations-intersectCount));
}
}
}


20 replies on “Super fast triangle/rectangle intersection test”
After checking if the triangle points are within the screen bounding box, I think you can check the other type of intersections by testing if any of the 4 points of the screen are inside the triangle. It would even work if the triangle contains the whole screen. But I don’t know if it would be finally faster.
I think lab9’s response does it. I am testing line segment intersection with arbitrary shapes by drawing the line into a Graphics object and hit-testing its bmp data against the shape — but I don’t imagine THAT’s faster!
this one seems interesting for fast point in triangle:
//www.blackpawn.com/texts/pointinpoly/default.html
hope that helps 🙂
Hi lab9, yeah that’s the barycentric technique I mentioned. The slow thing with that is all the vector maths and all the object property accessors. But please try it out – if you can get it to run fast, let me know!
Seb
just made a version.
it runs faster, but some triangles don’t appear correctly when none of the screen bounds are within the triangle. so still some work to make it right…
public function triangleTest(rect:Rectangle, vertex0:Point, vertex1:Point, vertex2:Point ) : Boolean
{
// YOU MUST LEAVE THESE DECLARATIONS; they simulate necessary data exchange within PV3D
l = rect.left;
r = rect.right;
t = rect.top;
b = rect.bottom;
x0 = vertex0.x;
y0 = vertex0.y;
x1 = vertex1.x;
y1 = vertex1.y;
x2 = vertex2.x;
y2 = vertex2.y;
if (x0 > l && x0 t && y0 l && x1 t && y1 l && x2 t && y2 y0);
t1 = int(x1 * m1 + c1 > y1);
t2 = int(x2 * m2 + c2 > y2);
lm0 = l * m0 + c0;
lm1 = l * m1 + c1;
lm2 = l * m2 + c2;
rm0 = r * m0 + c0;
rm1 = r * m1 + c1;
rm2 = r * m2 + c2;
if ( !(t0 ^ int( lm0 > t)) && !(t1 ^ int(lm1 > t)) && !(t2 ^ int(lm2 > t))) return true;
if (!(t0 ^ int( lm0 > b)) && !(t1 ^ int(lm1 > b)) && !(t2 ^ int(lm2 > b))) return true;
if ( !(t0 ^ int( rm0 > t)) && !(t1 ^ int(rm1 > t)) && !(t2 ^ int(rm2 > t))) return true;
if (!(t0 ^ int( rm0 > b)) && !(t1 ^ int(rm1 > b)) && !(t2 ^ int(rm2 > b))) return true;
return false;
}
Hey lab9, looks very interesting, but I think the code got garbled somewhere… did you put it on wonderfl?
here is the wonderfl version
//wonderfl.kayac.com/code/9ac50d76e60fb98ba5617a71d07f7c09a17e78cc
That is some bloody good optimisation work there on the vector maths – very impressed. But yes, sadly there are several cases where no points are inside either of the two shapes, and the line intersections would still be required after all… but let’s keep working!
You’re right, intersection is absolutely needed to make it work correctly.
I just tried an another version for intersection. It runs pretty well:
//wonderfl.kayac.com/code/40ad55a14049d30d08a5282252f2047f27476948
and an another version:
//wonderfl.kayac.com/code/1c3708bc3d5fa42c3d223cfd1091530a4aac8f14
all is done in the same function, so the code is pretty redondant, but runs really fast.
Tried to implement the simplest optimizations.
Check if one of the vertexes of the triangle is inside the rectangle and check if all vertexes are on one side of the rectangle. This filters out approximately 88% of triangles.
Obviously I still need to use your lineRectangleIntersect after that.
Seems to run slightly faster.
//wonderfl.kayac.com/code/6d3fe69ca3450a2ba452c0085aaedd6e8e339fa5
Surely we want to go the other way – only cull triangles where every point is off-screen – otherwise you see them disappearing and it looks clunky?
Thank you. This article is very good.
I did some coding today and offloaded the intersection test into a Pixel Bender filter.. naturally, it is slow as hell (takes 100 times as long) if you run it synchronously cause you have to create a new job each time the function runs..
But, if we can construct a new test that has 100000 random triangles drawn.. and the intersect test sets the triangle to green or red depending on if it is inside the Culling rectangle.. then we could make a test to take advantage of Pixel Benders ability to run asynchronously.
Though, I think that the small amount of calculations is probably just a bad fit for using a pixel bender filter.. the overhead in creating the new job may just be too much..
Kristof Neirynck, there is some error in your function. thanks!
# //if all points of the triangle are on one side of the rect
# if((l>x0 && l>x1 && l>x2)
# || (r<x0 && r<x1 && ry0 && t>y1 && t>y2)
# || (b<y0 && b<y1 && b<y2)
# ){
# return false;
# }
lab9, in your function for calculating the line equation y=mx+c, what if xb = xa ?
Thank you guys so much for this discussion: it /really/ cleared up some issues I had optimizing rendering in the 2.5D engine im creating in javascript.
I ported (very little work) lab9’s optimized version to javascript (//pastebin.com/XhgvBzVw) and applied it to map clipping. It speeds up clipping about 50% and basically allows me to deal with maps that are infinitely deep: I’m treating z-planes as rhomboids and the viewport as the AABB. So if I simply keep track of zplane metrics for the map I’m able to quickly tell which ones could possibly encroach into the viewport when it comes time to clip the map for viewing.
Again thanks for helping me out optimizing a solution to a problem I was probably ill-equiped to solve 😀 If you’re curious about my engine it’s on github: //github.com/ixtli/jsrpg
To handle the case where the screen rectangle is completely contained by the triangle, simply check whether the rectangle’s center point is contained by the triangle.
This merely requires using the orientation predicate three times, and checking that the sign is the same in all 3 cases (or 0, which means that the rectangle’s center is directly on the relevant triangle’s edge).